[ Home | Main Table Of Contents | Table Of Contents | Keyword Index ]
crimp(n) 0.2 doc "C Raster Image Manipulation Package"
Name
crimp - CRIMP - Manipulation and Processing
Synopsis
- package require Tcl 8.5
- package require Tk 8.5
- package require crimp ?0.2?
- package require crimp::core ?0.2?
- ::crimp histogram image
- ::crimp statistics basic image
- ::crimp statistics otsu stats
- ::crimp add image1 image2 ?scale? ?offset?
- ::crimp alpha blend foreground background alpha
- ::crimp alpha set image mask
- ::crimp alpha opaque image
- ::crimp alpha over foreground background
- ::crimp atan2 image1 image2
- ::crimp blank type width height value...
- ::crimp crop image ww hn we hs
- ::crimp cut image dx dy w h
- ::crimp decimate xy image factor kernel
- ::crimp decimate x image factor kernel
- ::crimp decimate y image factor kernel
- ::crimp degamma image y
- ::crimp difference image1 image2
- ::crimp downsample xy image factor
- ::crimp downsample x image factor
- ::crimp downsample y image factor
- ::crimp effect charcoal image
- ::crimp effect emboss image
- ::crimp effect sharpen image
- ::crimp expand const image ww hn we hs ?value...?
- ::crimp expand extend image ww hn we hs
- ::crimp expand mirror image ww hn we hs
- ::crimp expand replicate image ww hn we hs
- ::crimp expand wrap image ww hn we hs
- ::crimp fft forward image
- ::crimp fft backward image
- ::crimp filter ahe image ?-border spec? ?radius?
- ::crimp filter convolve image ?-border spec? kernel...
- ::crimp filter gauss discrete image sigma ?r?
- ::crimp filter gauss sampled image sigma ?r?
- ::crimp filter mean image ?-border spec? ?radius?
- ::crimp filter rank image ?-border spec? ?radius ?percentile??
- ::crimp filter stddev image ?-border spec? ?radius?
- ::crimp filter sobel x image
- ::crimp filter sobel y image
- ::crimp filter scharr x image
- ::crimp filter scharr y image
- ::crimp filter prewitt x image
- ::crimp filter prewitt y image
- ::crimp filter roberts x image
- ::crimp filter roberts y image
- ::crimp filter canny sobel image
- ::crimp filter canny deriche image
- ::crimp filter wiener image radius
- ::crimp gamma image y
- ::crimp gradient sobel image
- ::crimp gradient scharr image
- ::crimp gradient prewitt image
- ::crimp gradient roberts image
- ::crimp gradient polar cgradient
- ::crimp gradient visual pgradient
- ::crimp hypot image1 image2
- ::crimp integrate image
- ::crimp interpolate xy image factor kernel
- ::crimp interpolate x image factor kernel
- ::crimp interpolate y image factor kernel
- ::crimp invert image
- ::crimp logpolar image rwidth rheight ?xcenter? ?ycenter? ?corners?
- ::crimp matrix image matrix
- ::crimp max image1 image2
- ::crimp min image1 image2
- ::crimp montage horizontal ?-align top|center|bottom? ?-border spec? image...
- ::crimp montage vertical ?-align left|middle|right? ?-border spec? image...
- ::crimp morph dilate image
- ::crimp morph erode image
- ::crimp morph close image
- ::crimp morph open image
- ::crimp morph gradient image
- ::crimp morph igradient image
- ::crimp morph egradient image
- ::crimp morph tophatw image
- ::crimp morph tophatb image
- ::crimp morph toggle image
- ::crimp multiply image1 image2
- ::crimp noise random w h
- ::crimp noise saltpepper image ?density?
- ::crimp noise gaussian image ?mean? ?variance?
- ::crimp noise speckle image ?variance?
- ::crimp psychedelia width height frames
- ::crimp pyramid run image steps stepcmd
- <stepcmd> image
- ::crimp pyramid gauss image steps
- ::crimp pyramid laplace image steps
- ::crimp remap image map...
- ::crimp matchsize image1 image2
- ::crimp matchgeo image bbox
- ::crimp scale image scale
- ::crimp screen image1 image2
- ::crimp solarize image threshold
- ::crimp square image
- ::crimp subtract image1 image2 ?scale? ?offset?
- ::crimp threshold global above image threshold
- ::crimp threshold global below image threshold
- ::crimp threshold global inside image min max
- ::crimp threshold global outside image min max
- ::crimp threshold global middle image
- ::crimp threshold global mean image
- ::crimp threshold global median image
- ::crimp threshold global otsu image
- ::crimp threshold local image threshold...
- ::crimp upsample xy image factor
- ::crimp upsample x image factor
- ::crimp upsample y image factor
- ::crimp wavy image offset adj1 adjb
- ::crimp flip horizontal image
- ::crimp flip transpose image
- ::crimp flip transverse image
- ::crimp flip vertical image
- ::crimp resize ?-interpolate nneighbour|bilinear|bicubic? image w h
- ::crimp rotate cw image
- ::crimp rotate ccw image
- ::crimp rotate half image
- ::crimp warp field ?-interpolate nneighbour|bilinear|bicubic? image xvec yvec
- ::crimp warp projective ?-interpolate nneighbour|bilinear|bicubic? image transform
- ::crimp window image
- ::crimp convert 2grey32 image
- ::crimp convert 2grey16 image
- ::crimp convert 2grey8 image
- ::crimp convert 2float image
- ::crimp convert 2complex image
- ::crimp convert 2hsv image
- ::crimp convert 2rgba image
- ::crimp convert 2rgb image
- ::crimp convert 2rgb image
- ::crimp complex magnitude image
- ::crimp complex 2complex image
- ::crimp complex imaginary image
- ::crimp complex real image
- ::crimp complex conjugate image
- ::crimp join 2hsv hueImage satImage valImage
- ::crimp join 2rgba redImage greenImage blueImage alphaImage
- ::crimp join 2rgb redImage greenImage blueImage
- ::crimp join 2complex realImage imaginaryImage
- ::crimp join 2grey16 msbImage lsbImage
- ::crimp join 2grey32 mmsbImage lmsbImage mlsbImage llsbImage
- ::crimp split image
- ::crimp read pgm string
- ::crimp read ppm string
- ::crimp read strimj string ?colormap?
- ::crimp gradient grey8 from to size
- ::crimp gradient rgb from to size
- ::crimp gradient rgba from to size
- ::crimp gradient hsv from to size
- ::crimp register translation needle haystack
- ::crimp kernel make matrix ?scale? ?offset?
- ::crimp kernel fpmake matrix ?offset?
- ::crimp kernel transpose kernel
- ::crimp kernel image kernel
- ::crimp map arg...
- ::crimp mapof table
- ::crimp table compose f g
- ::crimp table eval wrap cmd
- ::crimp table eval clamp cmd
- <cmd> x
- ::crimp table degamma y
- ::crimp table gamma y
- ::crimp table gauss sigma
- ::crimp table identity
- ::crimp table invers
- ::crimp table linear wrap gain offset
- ::crimp table linear clamp gain offset
- ::crimp table log ?max?
- ::crimp table solarize threshold
- ::crimp table sqrt ?max?
- ::crimp table stretch min max
- ::crimp table threshold above threshold
- ::crimp table threshold below threshold
- ::crimp table threshold inside min max
- ::crimp table threshold outside min max
- ::crimp table fgauss discrete sigma ?r?
- ::crimp table fgauss sampled sigma ?r?
- ::crimp transform affine a b c d e f
- ::crimp transform chain transform...
- ::crimp transform identity
- ::crimp transform invert transform
- ::crimp transform projective a b c d e f g h
- ::crimp transform quadrilateral src dst
- ::crimp transform reflect line ?a? b
- ::crimp transform reflect x
- ::crimp transform reflect y
- ::crimp transform rotate theta ?center?
- ::crimp transform scale sx sy
- ::crimp transform shear sx sy
- ::crimp transform translate dx dy
- ::crimp::black_white_vertical
- ::crimp::bilateral_* image sigma-space sigma-range
- ::crimp::joint_bilateral_* image wimage sigma-space sigma-range
- ::crimp::color_combine image vector
- ::crimp::color_mix image matrix
- ::crimp::connected_components image 8connected
- ::crimp::connected_components_* image 8connected bgValue
- ::crimp::euclidean_distance_map_float image
- ::crimp::indicator_grey8_float image
- ::crimp::hough_grey8 image emptybucketcolor
- ::crimp::gaussian_01_float image derivative sigma
- ::crimp::gaussian_10_float image derivative sigma
- ::crimp::gaussian_blur_float image sigma
- ::crimp::gaussian_laplacian_float image sigma
- ::crimp::gaussian_gradient_mag_float image sigma
- ::crimp::map_2*_* image map
- ::crimp::map2_* image mapNimage... mapNcontrol...
- ::crimp::region_sum image radius
- ::crimp::exp_float image
- ::crimp::log_float image
- ::crimp::log10_float image
- ::crimp::offset_float image offset
- ::crimp::pow_float_float imageBase imageExponent
- ::crimp::scale_float image factor
- ::crimp::sqrt_float image
- ::crimp::non_max_suppression imageMagnitude imageAngle
- ::crimp::trace_hysteresis image low high
- ::crimp::window_* image
- ::crimp::window_* image
Description
This package, built on top of the crimp::core package provides the majority of CRIMPs power, manipulating and transforming images in a number of ways.
For a basic introduction of the whole CRIMP eco-system please read the CRIMP - Introduction to CRIMP (sic!). The basic concepts used here, like images, image types, etc. are described in the reference manpage for the CRIMP - Foundation. We will not repeat them here, but assume that the reader knows them already.
In the overall architecture this package resides in the middle layer of the system's architecture, between core and applications, as shown at
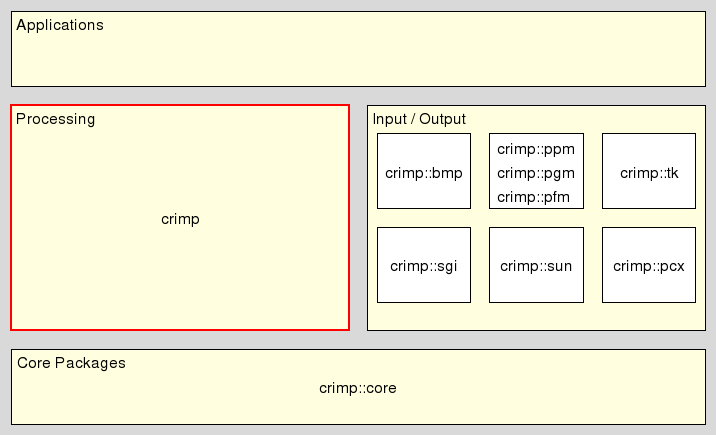
Note that the intended audience of this document are the users of crimp. Developers wishing to work on the internals of the package, but unfamiliar with them, should read ... instead.
API
Accessors
- ::crimp histogram image
This method returns a nested dictionary as its result. The outer dictionary is indexed by the names of the channels in the image. Its values, the inner dictionaries, are indexed by pixel value. The associated values are the number of pixels with that value.
The method supports all image types except "grey32". Under the current system the result would be a dictionary with 2^32 keys and values, taking up, roughly, 192 GiByte of memory in the worst case, and 96 GiByte in best case (all counter values shared in a single object).
- ::crimp statistics basic image
This method returns a nested dictionary as its result. The outer dictionary contains basic information about the image, see the list of keys below. The inner dictionaries hold data about each (color) channel in the image, namely histogram and derived data like minumum pixel value, maximum, etc.
- dimensions
2-element list holding image width and height, in this order.
- height
Image height as separate value.
- pixels
Number of pixels in the image, the product of its width and height.
- type
Type of the image.
- width
Image width as separate value.
- channels
List of the names for the channels in the image.
- channel
A dictionary mapping the names of the image's channels, as listed under key channels, to a dictionary holding the statistics for that channel.
- min
The minimal pixel value with a non-zero population.
- max
The maximal pixel value with a non-zero population.
- mean
The arithmetic mean (aka average) of pixel values.
- middle
The arithmetic mean of the min and max pixel values.
- median
The median pixel value.
- stddev
The standard deviation of pixel values.
- variance
The variance of pixel values, square of the standard deviation.
- histogram
A dictionary mapping pixel values to population counts.
- hf
The histogram reduced to the population counts, sorted by pixel value to direct indexing into the list by pixel values.
- cdf
The cumulative density function of pixel values. The discrete integral of hf.
- cdf255
Same as cdf, except scaled down so that the last value in the series is 255.
The method supports all image types except "grey32". Under the current system the result would contain internal dictionaries with 2^32 keys and values, taking up, roughly, 192 GiByte of memory in the worst case, and 96 GiByte in best case (all counter values shared in a single object).
- ::crimp statistics otsu stats
This method takes a dictionary of basic image statistics as generated by crimp statistics basic and returns an extended dictionary containing a threshold for image binarization computed by Otsu's method (See reference 2). Note that this threshold is computed separately for each channel and stored in the channel specific part of the dictionary, using the key otsu.
Manipulators
- ::crimp add image1 image2 ?scale? ?offset?
This method combines the two input images into a result image by performing a pixelwise addition (image1 + image2) followed by division through scale and addition of the offset. They default to 1 and 0 respectively, if they are not specified.
- ::crimp alpha blend foreground background alpha
This method takes two images of identical dimensions and a blending factor alpha and returns an image which is a mix of both, with each pixel blended per the formula
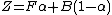
or, alternatively written
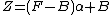
This means that the foreground is returned as is for "alpha == 255", and the background for "alpha == 0". I.e. the argument alpha controls the opacity of the foreground, with 1 and 0 standing for "fully opaque" and "fully transparent", respectively.
The following combinations of fore- and background image types are supported:
Result = Foreground Background ------ ---------- ---------- grey8 grey8 grey8 hsv hsv hsv rgb rgb grey8 rgb rgb rgb rgb rgb rgba rgba rgba grey8 rgba rgba rgb rgba rgba rgba ------ ---------- ----------- ::crimp alpha set image mask
This command takes two images, the input and a mask, and returns an image as result in which the mask is the alpha channel of the input. The result is therefore always of type rgba, as the only type supporting an alpha channel.
The input image can be of type rgb or rgba. In case of the latter the existing alpha channel is replaced, in case of the former an alpha channel is added.
For the mask images of type grey8 and rgba are accepted. In the case of the latter the mask's alpha channel is used as the new alpha channel, in case of the former the mask itself is used.
- ::crimp alpha opaque image
A convenience method over alpha set, giving the image a mask which makes it fully opaque.
- ::crimp alpha over foreground background
This method is similar to blend above, except that there is no global blending parameter. This information is taken from the "alpha" channel of the foreground image instead. The blending formula is the same, except that the alpha parameter is now a per-pixel value, and not constant across the image.
Due to the need for an alpha channel the foreground has to be of type rgba. For the background image the types rgb and rgba are supported.
- ::crimp atan2 image1 image2
This method combines the two input images into a result image by computing
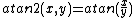
at each pixel.
The input is restricted to images of the single-channel types, i.e. float and grey{8,16,32}. The result is always of type float.
An application of this operation is the computation of a gradient's direction from two images representing a gradient in X and Y directions. For the full conversion of such cartesian gradients to a polar representation use the crimp hypot operation to compute the gradient's magnitude at each pixel.
- ::crimp blank type width height value...
This method returns a blank image of the given image type and dimensions. The values after the dimensions are the pixel values to fill the pixels in the image's channels with, per its type.
The method supports the image types rgb, rgba, hsv, float, fpcomplex, grey8, grey16, and grey32.
For the multi-channel types the method automatically extends the pixel values with 0 if not enough values were provided.
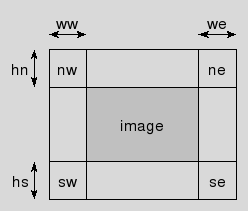
- ::crimp crop image ww hn we hs
This method is the counterpart to the expand family of methods, shrinking an image by removing a border. The size of this border is specified by the four arguments ww, hn, we, and hs which provide the number of pixels to remove from the named edge. See the image below for a graphical representation.
- ::crimp cut image dx dy w h
This method takes the rectangular region specified through its x/y position relative to the upper-left corner of the input image and its dimensions, and returns it as its own image.
Note that while both w and h are allowed to be 0, resulting in the return of an empty image, they are not allowed to be negative.
Further note that it is allowed to specify regions which address pixels outside of the input image. In the result these pixels will be set to 0 (meaning black, opaque, etc. as per the semantics of the image type).
The location of the result is the location of the input, suuitably modified by dx and dy.
- ::crimp decimate xy image factor kernel
- ::crimp decimate x image factor kernel
- ::crimp decimate y image factor kernel
This is a convenience method combining the two steps of filtering an image (via filter convolve), followed by a downsample step. See the method interpolate for the complementary operation.
Note that while the kernel argument for filter convolve is expected to be the 1D form of a separable low-pass filter no checks are made. The method simply applies both the kernel and its transposed form.
The method pyramid gauss is a user of this method.
- ::crimp degamma image y
This method takes an image, runs it through an inverse gamma correction with parameter y, and returns the corrected image as it result. This is an application of method remap, using the mapping returned by "map degamma y". This method supports all image types supported by the method remap.
- ::crimp difference image1 image2
This method combines the two input images into a result image by taking the pixelwise absolute difference (|image1 - image2|).
- ::crimp downsample xy image factor
- ::crimp downsample x image factor
- ::crimp downsample y image factor
This method returns an image containing only every factor pixel of the input image (in x, y, or both dimensions). The effect is that the input is shrunken by factor. It is the complement of method upsample.
Using the method as is is not recommended because the simple subsampling will cause higher image frequencies to alias into the reduced spectrum, causing artifacts to appear in the result. This is normally avoided by running a low-pass filter over the image before doing downsampling, removing the problematic frequencies.
The decimate method is a convenience method combining these two steps into one.
- ::crimp effect charcoal image
This method applies a charcoal effect to the image, i.e. it returns a grey8 image showing the input as if it had been drawn with a charcoal pencil.
- ::crimp effect emboss image
This method applies an embossing effect to the image, i.e. it returns an image of the same type as the input showing the input as if it had been embossed into a metal plate with a stencil of some kind.
- ::crimp effect sharpen image
This method sharpens the input image, i.e. returns an image of the same type as the input in which the input's edges are emphasized.
- ::crimp expand const image ww hn we hs ?value...?
- ::crimp expand extend image ww hn we hs
- ::crimp expand mirror image ww hn we hs
- ::crimp expand replicate image ww hn we hs
- ::crimp expand wrap image ww hn we hs
This set of methods takes an image and expands it by adding a border. The size of this border is specified by the four arguments ww, hn, we, and hs which provide the number of pixels to add at the named edge. See the image below for a graphical representation.

The contents of the border's pixels are specified via the border type, the first argument after expand, as per the list below.
- const
The additional values specify the values to use for the color channels of the image. Values beyond the number of channels in the image are ignored. Missing values are generated by replicating the last value, except for the alpha channel, which will be set to 255. If no values are present they default to 0.
- extend
This is a combination of mirror and replicate. The outside pixels are the result of subtracting the outside pixel for mirror from the outside pixel for replicate (and clamping to the range [0...255]).
- mirror
The outside pixels take the value of the associated inside pixels, found by reflecting its coordinates along the relevant edges.
- replicate
The outside pixels take the value of the associated edge pixels, i.e. replicating them into the border.
- wrap
The outside pixels take the value of the associated inside pixels, found by toroidial (cyclic) wrapping its coordinates along the relevant edges. This is also called tiling.
- ::crimp fft forward image
- ::crimp fft backward image
These two methods implement 2D FFT (forward) and inverse FFT (backward).
The input is restricted to images of the single-channel types, i.e. float, grey{8,16,32} and fpcomplex. The result is always of type float for input images other than fpcomplex, which returns an image of the same type instead.
The former means that it is necessary to split rgb, etc. images into their channels before performing an FFT, and that results of an inverse FFT have to be joined. See the methods split and join for the relevant operations and their syntax.
The latter means that a separate invokation of method convert 2grey8 is required when reconstructing an image by inverting its FFT.
- ::crimp filter ahe image ?-border spec? ?radius?
This method performs adaptive histogram equalization to enhance the contrast of the input image. Each pixel undergoes regular histogram equalization, with the histogram computed from the pixels in the NxN square centered on it, where "N = 2*radius+1".
The default radius is 3, for a 7x7 square.
- ::crimp filter convolve image ?-border spec? kernel...
This method runs the series of filters specified by the convolution kernels over the input and returns the filtered result. See the method kernel and its sub-methods for commands to create and manipulate suitable kernels.
The border specification determines how the input image is expanded (see method expand) to compensate for the shrinkage introduced by the filter itself. The spec argument is a list containing the name of the sub-method of expand to use, plus any additional arguments this method may need, except for the size of the expansion.
By default a black frame is used as the border, i.e. "spec == {const 0}".
- ::crimp filter gauss discrete image sigma ?r?
- ::crimp filter gauss sampled image sigma ?r?
These methods apply a discrete or sampled gaussian blur with parameters sigma and kernel radius to the image. If the radius is not specified it defaults to the smallest integer greater than "3*sigma".
- ::crimp filter mean image ?-border spec? ?radius?
This method applies a mean filter with radius to the image. I.e. each pixel of the result is the mean value of all pixels in the NxN square centered on it, where "N = 2*radius+1".
The default radius is 3, for a 7x7 square.
NOTE. As the mean is known to be in the range defined by the channel this method automatically converts float results back to the channel type. This introduces rounding / quantization errors. As a result of this price being paid the method is able to handle multi-channel images, by automatically splitting, processing, and rejoining its channels.
The method filter stddev on the other makes the reverse tradeoff, keeping precision, but unable to handle multi-channel images.
- ::crimp filter rank image ?-border spec? ?radius ?percentile??
This method runs a rank-filter over the input and returns the filtered result.
The border specification determines how the input image is expanded (see method expand) to compensate for the shrinkage introduced by the filter itself. The spec argument is a list containing the name of the sub-method of expand to use, plus any additional arguments this method may need, except for the size of the expansion.
By default a black frame is used as the border, i.e. "spec == {const 0}".
The radius specifies the (square) region around each pixel which is taken into account by the filter, with the pixel value selected according to the percentile. The filter region of each pixel is a square of dimensions "2*radius+1", centered around the pixel.
These two values default to 3 and 50, respectively.
Typical applications of rank-filters are min-, max-, and median-filters, for percentiles 0, 100, and 50, respectively.
Note that percentiles outside of the range 0...100 make no sense and are clamped to this range.
- ::crimp filter stddev image ?-border spec? ?radius?
This method applies a stand deviation filter with radius to the image. I.e. each pixel of the result is the standard deviation of all pixel values in the NxN square centered on it, where "N = 2*radius+1".
The default radius is 3, for a 7x7 square.
NOTE. As the standard deviation is often quite small and its precision important the result of this method is always an image of type float. Because of this this method is unable to handle multi-channel images as the results of processing their channels cannot be joined back together for the proper type.
The method filter mean on the other hand makes the reverse tradeoff, handling multi-channel images, but dropping precision.
- ::crimp filter sobel x image
- ::crimp filter sobel y image
- ::crimp filter scharr x image
- ::crimp filter scharr y image
- ::crimp filter prewitt x image
- ::crimp filter prewitt y image
- ::crimp filter roberts x image
- ::crimp filter roberts y image
- ::crimp filter canny sobel image
- ::crimp filter canny deriche image
These methods are convenience methods implementing a number of standard convolution filters using for edge detection and calculation of image gradients.
See the crimp gradient methods for users of these filters.
Also note that the x methods emphasize gradient in the horizontal direction, and thus highlight vertical lines, and vice versa for y.
- ::crimp filter wiener image radius
This method filters an image that has been degraded by constant power additive noise. It uses a pixelwise adaptive Filter method based on statistics estimated from a local neighborhood of each pixel. The default value for radius is 2
- ::crimp gamma image y
This method takes an image, runs it through a gamma correction with parameter y, and returns the corrected image as it result. This is an application of method remap, using the mapping returned by "map gamma y". This method supports all image types supported by the method remap.
- ::crimp gradient sobel image
- ::crimp gradient scharr image
- ::crimp gradient prewitt image
- ::crimp gradient roberts image
These methods generate two gradient images for the input image, in the X- and Y-directions, using different semi-standard filters. I.e. the result is a cartesian representation of the gradients in the input. The result is a 2-element list containing the X- and Y-gradient images, in this order.
- ::crimp gradient polar cgradient
This method takes a gradient in cartesian representation (as returned by the above methods) and converts it to polar representation, i.e. magnitude and angle. The result of the method is a 2-element list containing two float images, the magnitude and angle, in this order. The angle is represented in degrees running from 0 to 360.
- ::crimp gradient visual pgradient
This method takes a gradient in polar representation (as returned by method gradient polar) and converts it into a color image (rgb) visualizing the gradient.
The visualization is easier to understand in HSV space tough, with the angle mapped to Hue, i.e. color, magnitude to Value, and Saturation simply at full.
- ::crimp hypot image1 image2
This method combines the two input images into a result image by computing
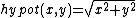
at each pixel.
The input is restricted to images of the single-channel types, i.e. float and grey{8,16,32}. The result is always of type float.
An application of this operation is the computation of the gradient magnitude from two images representing a gradient in X and Y directions. For the full conversion of such cartesian gradients to a polar representation use the crimp atan2 operation to compute the gradient's direction at each pixel.
- ::crimp integrate image
This method takes any single-channel image, i.e. of types float and grey{8,16,32}, and returns its integral, i.e. a summed area table. The type of the result is always of type float.
- ::crimp interpolate xy image factor kernel
- ::crimp interpolate x image factor kernel
- ::crimp interpolate y image factor kernel
This is a convenience method combining the two steps of an upsample, followed by a filter step (via filter convolve). See the method decimate for the complementary operation.
Note that while the kernel argument for filter convolve is expected to be 1D form of a separable low-pass filter no checks are made. The method simply applies both the kernel and its transposed form.
The methods pyramid gauss and pyramid laplace are users of this method.
- ::crimp invert image
This method takes an image, runs it through the inverse function, and returns the modified image as it result. This is an application of method remap, using the mapping returned by "map inverse". This method supports all image types supported by the method remap.
- ::crimp logpolar image rwidth rheight ?xcenter? ?ycenter? ?corners?
This method takes an image and returns the log-polar transformation of the input. This means that in the result each pixel is described by an angle and the logarithm of the distance to a chosen point.
The angle is plotted on the x-axis of the result, as fraction or multiples of degrees, depending on the chosen resolution rwidth. A value of 360, for example, provides a resolution of 1 degree in the result. The angle is counted from 0 due right (the positive x-axis of the input) counterclockwise.
The log of the distance is plotted on the y-axis of the result, with a precision of rheight.
The center point is specified as offset xcenter, ycenter from the center of the input image. I.e. the defaults of (0, 0) for both, when not specified, refer to the center of the input.
The optional flag corners specifies whether to include the corners of the input in the result (true), or not (false). This defaults to true, including the corners.
- ::crimp matrix image matrix
This method takes an image and a 3x3 matrix specified as nested Tcl list (row major order), applies the projective transform represented by the matrix to the image and returns the transformed image as its result.
Notes: It is currently unclear how the output pixel is computed (nearest neighbour, bilinear, etc.) (code inherited from AMG). This requires more reading, and teasing things apart. The transfomred image is clipped to the dimensions of the input image, i.e. pixels from the input may be lost, and pixels in the output may be unset as their input would come from outside of the input.
The operation supports only images of type rgba, and returns images of the same type.
- ::crimp max image1 image2
This method combines the two input images into a result image by taking the pixelwise maximum.
- ::crimp min image1 image2
This method combines the two input images into a result image by taking the pixelwise minimum.
- ::crimp montage horizontal ?-align top|center|bottom? ?-border spec? image...
- ::crimp montage vertical ?-align left|middle|right? ?-border spec? image...
The result of these methods is an image where the input images have been placed adjacent to each from left to right (horizontal), or top to bottom (vertical). The input images have to have the same type.
There is no need however for them to have the same height, or width, respectively. When images of different height (width) are used the command will expand them to their common height (width), which is the maximum of all heights (widths). The expansion process is further governed by the values of the -align and -border options, with the latter specifying the form of the expansion (see method expand for details), and the first specifying how the image is aligned within the expanded space.
The spec argument of -border is a list containing the name of the sub-method of expand to use, plus any additional arguments this method may need, except for the size of the expansion.
The default values for -align are center and middle, centering the image in the space. The default for the -border is a black frame, i.e. "spec == {const 0}".
- ::crimp morph dilate image
- ::crimp morph erode image
These two methods implement the basic set of morphology operations, erosion, and dilation using a flat 3x3 brick as their structuring element. For grayscale, which we have here, these are, mathematically, max and min rank-order filters, i.e.
dilate = filter rank 1 99.99 (max) erode = filter rank 1 0.00 (min)The above definitions assume that background is black, and foreground/object anything but black, usually white. Then it is easy to see that dilate expands the foreground/white, and erode expands background/black.
- ::crimp morph close image
- ::crimp morph open image
These two methods add to the basic set of morphology operations, opening and closing. In terms of erosion and dilation:
close = erode o dilate open = dilate o erode- ::crimp morph gradient image
The morphological gradient is defined as
[dilate $image] - [erode $image]This can also be expressed as the sum of the external and internal gradients, see below.
- ::crimp morph igradient image
The morphological internal gradient is defined as
$image - [erode image]- ::crimp morph egradient image
The morphological external gradient is defined as
[dilate $image] - $image- ::crimp morph tophatw image
The white tophat transformation is defined as
$image - [open $image]See References 3 to 5 (page 32). This is a greyscale morphology operation which does not properly apply to binary images.
- ::crimp morph tophatb image
The black tophat transformation is defined as
[close $image] - $imageSee References 3 to 5 (page 33). This is a greyscale morphology operation which does not properly apply to binary images.
- ::crimp morph toggle image
The toggle map is defined as
0.5 * ([erode $image] + [dilate $image])See References 5, pages 34 and 35. This is a greyscale morphology operation to sharpen edges.
- ::crimp multiply image1 image2
This method combines the two input images into a result image by performing a pixelwise multiplication. Note that the result of each multiplication is divided by 255 to scale it back into the range [0...255].
- ::crimp noise random w h
This method creates an image of type float with the specified dimensions. The pixels are set to random values in the interval [0...1].
- ::crimp noise saltpepper image ?density?
- ::crimp noise gaussian image ?mean? ?variance?
- ::crimp noise speckle image ?variance?
These methods add noises of different types to the given image.
saltpepper adds salt and pepper noise of the specified density. This density must be in the range [0...1]. If not specified it defaults to 0.05.
gaussian adds gaussian noise of the specified mean and variance to the image. If not specified the mean and variance default to 0 and 0.05, respectively. Both must be in the range [0...1].
speckle adds multiplicative noise of the specified variance to the image. This variance must be in the range [0...1]. If not specified it defaults to 0.05.
- ::crimp psychedelia width height frames
This method creates an rgba image of the specified dimensions according to an algorithm devised by Andrew M. Goth. The frames argument specifies how many images are in the series.
Attention: This method keeps internal global state, ensuring that each call returns a slightly different image. Showing a series of such images as animation provides an effect similar to a lava lamp or hallucination.
- ::crimp pyramid run image steps stepcmd
This method provides the core functionality for the generation of image pyramids. The command prefix stepcmd is run steps times, first on the image, then on the result of the previous step.
The assumed signature of stepcmd is
- <stepcmd> image
which is expected to return a list of two elements. The first element (result) is added to the pyramid in building, whereas the second element (iter) is used in the next step as the input of the step command.
The final result of the method is a list containing the input image as its first element, followed by the results of the step function, followed by the iter element returned by the last step, "steps+2" images in total.

- ::crimp pyramid gauss image steps
This method generates a gaussian image pyramid steps levels deep and returns it as a list of images.
The first image in the result is the input, followed by steps successively smaller images, each decimated by a factor two compared to its predecessor, for a total length of "steps+1" images.
The convolution part of the decimation uses
1/16 [1 4 6 4 1]
as its kernel.

- ::crimp pyramid laplace image steps
This method generates a laplacian image pyramid steps levels deep and returns it as a list of images.
The first image in the result is the input, followed by steps band pass images (differences of gaussians). The first band pass has the same size as the input image, and each successor is decimated by two. This is followed by one more image, the gaussian of the last step. This image is decimated by two compared to the preceding bandpass image. In total the result contains "steps+2" images.
The convolution part of the decimation uses
1/16 [1 4 6 4 1]
as its kernel. The internal interpolation used to generate the band pass images (resynthesis) doubles the weights of this kernel for its convolution step.
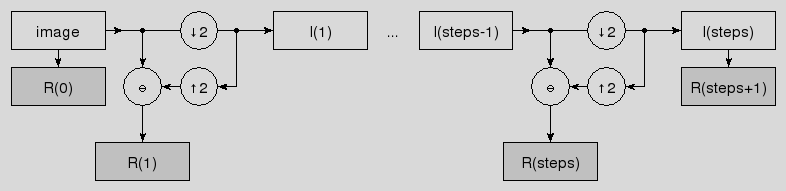
- ::crimp remap image map...
This method is the core primitive for the per-pixel transformation of images, with each pixel (and channels within, if any) handled independently of all others. Applications of this operator provided by this package are (inverse) gamma correction, pixel inversion, and solarization. Many more are possible, especially when considering other colorspaces like HSV. There, for example, it is possible change the saturation of pixels, or shift the hue in arbitrary manner.
Beyond the input image to transform one or more maps are specified which define how each pixel value in the input is mapped to a pixel value in the output. The command will accept at most that many maps as the input image has channels. If there are less maps than channel the last map specified is replicated to cover the other channels. An exception of this is the handling of the alpha channel, should the input image have such. There a missing map is handle as identity, i.e. the channel copied as is, without changes.
The maps are not Tcl data structures, but images themselves. They have to be of type grey8, and be of dimension 256x1 (width by height).
The crimp map ... methods are sources for a number of predefined maps, whereas the mapof method allows the construction of maps from Tcl data structures, namely lists of values.
This method supports all image types with one or more single-byte channels, i.e. all but grey16, grey32, float, and bw.
- ::crimp matchsize image1 image2
This method takes two images, forces them to be of the same size by expanding the smaller dimensions with black pixels, and then returns a list of the expanded images. The images in the result are in the same order as as arguments.
- ::crimp matchgeo image bbox
This method takes an image and a bounding box (list of x, y, w, and h), and expands the image with black pixels to match the box. The result of the expansion is returned.
An error is thrown if the image is not fully contained within the bounding box.
- ::crimp scale image scale
This method performs a pixel-wise multiplication of the image with a constant factor. It is currently supported by all greyN image types, plus the types float and fpcomplex. The first accept an integer scaling factor, whereas the last two accept any floating point number.
- ::crimp screen image1 image2
This method combines the two input images by inverting the multiplication of the inverted input images. I.e.
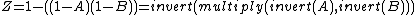
- ::crimp solarize image threshold
This method takes an image, runs it through the solarize function with parameter threshold, and returns the modified image as it result. This is also known as the sabattier effect. This is an application of method remap, using the mapping returned by "map solarize threshold". This method supports all image types supported by the method remap.
- ::crimp square image
This is a convenience method equivalent to "crimp multiply image image".
- ::crimp subtract image1 image2 ?scale? ?offset?
This method combines the two input images into a result image by performing a pixelwise subtraction (image1 - image2) followed by division through scale and addition of the offset. They default to 1 and 0 respectively, if they are not specified.
- ::crimp threshold global above image threshold
This method takes an image, runs it through the threshold above function with parameter threshold, and returns the modified image as it result. As the result only contains black and white, i.e. 2 colors, this process is also called binarization or foreground/background segmentation. This is an application of method remap, using the mapping returned by "map threshold above threshold". This method supports all image types supported by the method remap.
- ::crimp threshold global below image threshold
This method takes an image, runs it through the threshold below function with parameter threshold, and returns the modified image as it result. As the result only contains black and white, i.e. 2 colors, this process is also called binarization, or foreground/background segmentation. This is an application of method remap, using the mapping returned by "map threshold below threshold". This method supports all image types supported by the method remap.
- ::crimp threshold global inside image min max
This method takes an image, runs it through the threshold inside function with parameters min and max, and returns the modified image as it result. As the result only contains black and white, i.e. 2 colors, this process is also called binarization or foreground/background segmentation. This is an application of method remap, using the mapping returned by "map threshold above threshold". This method supports all image types supported by the method remap.
- ::crimp threshold global outside image min max
This method takes an image, runs it through the threshold outside function with parameters min and max, and returns the modified image as it result. As the result only contains black and white, i.e. 2 colors, this process is also called binarization, or foreground/background segmentation. This is an application of method remap, using the mapping returned by "map threshold below threshold". This method supports all image types supported by the method remap.
- ::crimp threshold global middle image
- ::crimp threshold global mean image
- ::crimp threshold global median image
- ::crimp threshold global otsu image
These four methods are convenience methods layered on top of crimp threshold global below. They compute the value(s) to perform the thresholding with from the global statistics of the input image, with the element taken named by the method. For reference see the documentation of method crimp statistics .... Note that they treat each color channel in the image separately.
- ::crimp threshold local image threshold...
This method takes an image and one or more threshold maps and returns an image where all pixels of the input which were larger or equal to the corresponding pixel in the map are set to black. All other pixels are set to white. Each map is applied to one color channel of the input image. If there are too many maps the remainder is ignored. If there are not enough maps the last map is replicated.
This is the core for all methods of non-global binarization, i.e. foreground/background segmentation. Their differences are just in the calculation of the maps.
This method supports all image types with one or more single-byte channels, i.e. all but grey16, grey32, and bw.
- ::crimp upsample xy image factor
- ::crimp upsample x image factor
- ::crimp upsample y image factor
This method returns an image inserting factor black pixels between each pixel of the input image (in x, y, or both dimensions). The effect is that the input is expanded by factor. It is the complement of method downsample.
Using the method as is is not recommended because this simple upsampling will cause copies of the image to appear at the higher image frequencies in the expanded spectrum. This is normally avoided by running a low-pass filter over the image after the upsampling, removing the problematic copies.
The interpolate method is a convenience method combining these two steps into one.
- ::crimp wavy image offset adj1 adjb
This method processes the input image according to an algorithm devised by Andrew M. Goth, according to the three parameters offset, adj1, and adjb, and returns the modified image as its result.
The operation supports only images of type rgba, and returns images of the same type.
- ::crimp flip horizontal image
- ::crimp flip transpose image
- ::crimp flip transverse image
- ::crimp flip vertical image
This set of methods performs mirroring along the horizontal, vertical and diagonal axes of the input image, returning the mirrored image as their output. Transpose mirrors along the main diagonal, transverse along the secondary diagonal. These two methods also exchange width and height of the image in the output.
The methods currently support the image types rgb, rgba, hsv, and grey8.
- ::crimp resize ?-interpolate nneighbour|bilinear|bicubic? image w h
This method takes the input image and resizes it to the specified width w and height h. In constrast to cut this is not done by taking part of the image in the specified size, but by scaling it up or down as needed. In other words, this method is a degenerate case of a projective transform as created by the transform methods and used by method warp projective (see below).
Like the aforementioned general method this method supports all the possible interpolation types, i.e. nearest neighbour, bilinear, and bicubic. By default bilinear interpolation is used, as a compromise between accuracy and speed.
- ::crimp rotate cw image
- ::crimp rotate ccw image
This set of methods rotates the image in steps of 90 degrees, either clockwise and counter to it.
- ::crimp rotate half image
This methods rotates the image a half-turn, i.e. 180 degrees.
- ::crimp warp field ?-interpolate nneighbour|bilinear|bicubic? image xvec yvec
This method takes an input image and two images the size of the expected result which provide for each pixel in the result the coordinates to sample in the input to determine the result's color.
This allows the specification of any possible geometric transformation and warping, going beyond even projective transformations.
The two images providing the coordinate information have to be of the same size, which is also the size of the returned result. The type of the result is however specified through the type of the input image.
The method supports all the possible interpolation types, i.e. nearest neighbour, bilinear, and bicubic. By default bilinear interpolation is used, as a compromise between accuracy and speed.
- ::crimp warp projective ?-interpolate nneighbour|bilinear|bicubic? image transform
This method accepts a general projective transform as created by the transform methods, applies it to the input image and returns the projected result.
Like the resize method above this method supports all the possible interpolation types, i.e. nearest neighbour, bilinear, and bicubic. By default bilinear interpolation is used, as a compromise between accuracy and speed.
Note that the returned result image is made as large as necessary to contain the whole of the projected input. Depending on the transformation this means that parts of the result can be black, coming from outside of the boundaries of the input. Further, the origin point of the result may conceptually be inside or outside of the result instead of at the top left corner, because of pixels in the input getting projected to negative coordinates. To handle this situation the result will contain the physical coordinates of the conceptual origin point in its meta data, under the hierarchical key crimp origin.
- ::crimp window image
This method takes an image, applies a windowing function to it that fades the pixels to black towards the edges, and returns the windowed result.
Converters
- ::crimp convert 2grey32 image
- ::crimp convert 2grey16 image
- ::crimp convert 2grey8 image
- ::crimp convert 2float image
- ::crimp convert 2complex image
- ::crimp convert 2hsv image
- ::crimp convert 2rgba image
- ::crimp convert 2rgb image
- ::crimp convert 2rgb image
This set of methods all convert their input image to the specified type and returns it as their result. All converters accept an image of the destination type as input and will pass it through unchanged.
The converters returning a grey8 image support float, rgb and rgba as their input. For multi-channel input they use the ITU-R 601-2 luma transform to merge the color channels.
The converters returning a grey16, grey32 image support only float as their input.
The converters to HSV support rgb and rgba as their input as well.
The conversion to rgba accepts only hsv as input, adding a blank (fully opaque) alpha channel. For more control over the contents of an image's alpha channel see the methods setalpha and join rgba.
The conversion to rgb accepts both rgba and hsv images as input.
The conversion to float supports only fpcomplex as input. It simply strips the imaginary part of the input.
The conversion to fpcomplex accepts float, grey8, grey16, and grey32 as input, and adds a constant 0 imaginary part.
- ::crimp complex magnitude image
This method takes an image of type fpcomplex as input and returns an image of type float containing the pixel-wise magnitude of the input.
- ::crimp complex 2complex image
This method takes an image of type float as input and returns an image of type fpcomplex with each pixel's real part containing the input, and the imaginary part set to 0.
This method is an alias for crimp convert 2complex.
- ::crimp complex imaginary image
This method takes an image of type fpcomplex as input and returns an image of type float containing the pixel-wise imaginary part of the input.
- ::crimp complex real image
This method takes an image of type fpcomplex as input and returns an image of type float containing the pixel-wise real part of the input.
This method is an alias for crimp convert 2float as applied to images of type fpcomplex.
- ::crimp complex conjugate image
This method takes an image of type fpcomplex as input and returns an image of the same type containing the pixel-wise complex conjugate of the input.
- ::crimp join 2hsv hueImage satImage valImage
- ::crimp join 2rgba redImage greenImage blueImage alphaImage
- ::crimp join 2rgb redImage greenImage blueImage
- ::crimp join 2complex realImage imaginaryImage
- ::crimp join 2grey16 msbImage lsbImage
- ::crimp join 2grey32 mmsbImage lmsbImage mlsbImage llsbImage
This set of methods is the complement of method split. Each takes a set of grey8 images and fuses them together into an image of the given type, with each input image becoming one channel of the fusing result, which is returned as the result of the command. All input images have to have the same dimensions.
The command join 2complex is an exception regarding the input. It accepts images of type float, not grey8.
The commands join 2grey* are slightly different too. As the result has only one color channel, what is to join ? Their pixels are multi-byte, 2 and 4 respectively. The input images are not color channel, but become the msb and lsb of the respective pixel in the result.
- ::crimp split image
This method takes an image of one of the multi-channel types, i.e. rgb, rgba, hsv, and fpcomplex and returns a list of grey8 images, each of which contains the contents of one of the channels found in the input image.
The input image type fpcomplex is an exception regarding the output. It returns images of type float, not grey8.
The method is also able to take an image of one of the single-channel multi-byte types, i.e. grey16, and grey32 and returns a list of 2 (4) grey8 images, each of which contains one of the bytes a pixel is made out of, in msb to lsb order.
The channel images in the result are provided in the same order as they are accepted by the complementary join method, see above.
I/O commands
- ::crimp read pgm string
This method returns an image of type grey8 containing the data of the portable grey map (PGM) stored in the string. The method recognizes images in both plain and raw sub-formats.
- ::crimp read ppm string
This method returns an image of type rgb containing the data of the portable pix map (PPM) stored in the string. The method recognizes images in both plain and raw sub-formats.
- ::crimp read strimj string ?colormap?
This method returns an image of type rgba containing the data of the strimj (string image) (See http://wiki.tcl.tk/1846) stored in the string.
The caller can override the standard mapping from pixel characters to colors by specifying a colormap. This argument is interpreted as dictionary mapping characters to triples of integers in the range [0...255], specifying the red, green, and blue intensities.
An example of a strimj is:
@...@.......@.@...... @...@.......@.@...... @...@..@@@..@.@..@@@. @@@@@.@...@.@.@.@...@ @...@.@@@@@.@.@.@...@ @...@.@.....@.@.@...@ @...@.@...@.@.@.@...@ @...@..@@@..@.@..@@@.
Support
- ::crimp gradient grey8 from to size
- ::crimp gradient rgb from to size
- ::crimp gradient rgba from to size
- ::crimp gradient hsv from to size
This set of methods takes two "color" (pixel value) arguments and returns an image of height 1 and width size containing a gradient interpolating between these two colors, with from in the pixel at the left (x == 0) and to at the right (x == size-1).
size has to be greater than or equal to 2. An error is thrown if that restriction is not met.
The resulting image has the type indicated in the method name. This also specifies what is expected as the contents of the arguments from and to. For grey8 these are simple pixel values in the range 0...255 whereas for the types rgb and hsv the arguments are triples (3-element lists) specifying the R, G, and B (and H, S, and V respectively) values.
- ::crimp register translation needle haystack
This method takes two images which are translated copies of each other and returns a dictonary containing the two keys Xshift and Yshift, which together specify the translation to apply to the needle to place it in the haystack.
- ::crimp kernel make matrix ?scale? ?offset?
This method takes a matrix of weights and an optional scale factor and returns a structure containing the associated convolution kernel, ready for use by method filter convolve.
If scale is left unspecified it defaults to the sum of all weights in the matrix.
If offset is left unspecified it defaults to 128 if the sum of weights is 0, and 0 else. In effect zero-sum kernels, like the basic edge-detectors, are shifted so that results in the range -128..127 correspond to 0..255.
The matrix has the same general format as the pixel matrix for method read tcl grey8, i.e. a list of lists (rows) of values, and is treated in the same way, i.e. the number of columns is the maxium length over the row lists, and shorter lists are padded with 128. The values are expected to be integer numbers in the range -128..127.
- ::crimp kernel fpmake matrix ?offset?
This method is like kernel make except that the generated kernel is based on floating-point values. Because of this it is not accpeting a scale argument either, it is expected that the kernel weights already have the proper sum.
The matrix has the same general format as the pixel matrix for method read tcl float, i.e. a list of lists (rows) of values, and is treated in the same way, i.e. the number of columns is the maxium length over the row lists, and shorter lists are padded with 255. The values are expected to be floating-point numbers.
- ::crimp kernel transpose kernel
This method takes a kernel as returned by the method kernel make and returns a transposed kernel, i.e. one where the x- and y-axes are switched. For example
(1) (2) {1 2 4 2 1} ==> (4) (2) (1)This method is its own inverse, i.e. application to its result returns the original input, i.e.
[transpose [transpose $K]] == $K- ::crimp kernel image kernel
This method extracts and returns the internal image used to store the kernel's coefficients.
- ::crimp map arg...
This method accepts the same sub-methods and arguments as are accepted by the table method below. In contrast to table the result is not a list of values, but a map image directly suitable as argument to the remap method.
- ::crimp mapof table
This method accepts a list of 256 values, constructs a map image directly suitable as argument to the remap method, and returns this map image as its result.
- ::crimp table compose f g
This accepts two lookup tables (aka functions) specified as lists of 256 values, constructs the composite function f(g(x)), and then returns this new function as its result.
- ::crimp table eval wrap cmd
- ::crimp table eval clamp cmd
This method returns a list of 256 values, the result of running the values 0 to 255 through the function specified by the command prefix cmd. The results returned by the command prefix are rounded to the nearest integer and then forced into the domain [0..255] by either wrapping them around (modulo 256), or clamping them to the appropriate border, i.e 0, and 255 respectively.
The signature of the command prefix is
- <cmd> x
which is expected to return a number in the range [0..255]. While the result should be an integer number it is allowed to be a float, the caller takes care to round the result to the nearest integer.
- ::crimp table degamma y
This method returns a list of 256 values, the result of running the values 0 to 255 through the inverse gamma correction with parameter y. This inverse correction, defined in the domain of [0..1] for both argument and result, is defined as:

Scaling of argument and result into the domain [0..255] of pixel values, and rounding results to the nearest integer, causes the actual definition used to be
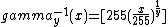
- ::crimp table gamma y
This method returns a list of 256 values, the result of running the values 0 to 255 through the gamma correction with parameter y. This correction, defined in the domain of [0..1] for both argument and result, is defined as:
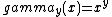
Scaling of argument and result into the domain [0..255] of pixel values, and rounding results to the nearest integer, causes the actual definition used to be
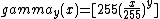
- ::crimp table gauss sigma
This method returns a list of 256 values, the result of running the values 0 to 255 through the sampled gauss function with parameter sigma. This function is defined as:
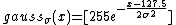
- ::crimp table identity
This method returns a list of 256 values, the result of running the values 0 to 255 through the identity function, which is defined as
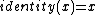
- ::crimp table invers
This method returns a list of 256 values, the result of running the values 0 to 255 through the inverse function, which is defined as
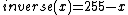
- ::crimp table linear wrap gain offset
- ::crimp table linear clamp gain offset
This method returns a list of 256 values, the result of running the values 0 to 255 through a simple linear function with parameters gain (the slope) and offset. The results are rounded to the nearest integer and then forced into the domain [0..255] by either wrapping them around (modulo 256), or clamping them to the appropriate border, i.e 0, and 255 respectively. Thus the relevant definitions are
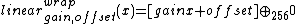 for the wrapped case, and
for the wrapped case, and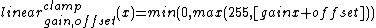 when clamping.
when clamping.- ::crimp table log ?max?
This method returns a list of 256 values, the result of running the values 0 to 255 through the log-compression function with parameter max. This parameter is the maximum pixel value the function is for, this value, and all larger will be mapped to 255. This function is defined as:
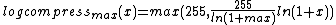
- ::crimp table solarize threshold
This method returns a list of 256 values, the result of running the values 0 to 255 through the solarize function, with parameter threshold. This function is defined as:
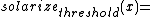
Note how the function is the identity for values under the threshold, and the inverse for values at and above it. Its application to an image produces what is known as either solarization or sabattier effect.
- ::crimp table sqrt ?max?
This method returns a list of 256 values, the result of running the values 0 to 255 through the sqrt-compression function with parameter max. This parameter is the maximum pixel value the function is for, this value, and all larger will be mapped to 255. This function is defined as:
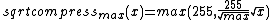
- ::crimp table stretch min max
This is a convenience method around table linear which maps min to 0, and max to 255, with linear interpolation in between. Values below min and above max are clamped to 0 and 255 respectively.
- ::crimp table threshold above threshold
This method returns a list of 256 values, the result of running the values 0 to 255 through a thresholding (or binarization) function, with parameter threshold. This function is defined as:
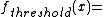
- ::crimp table threshold below threshold
This method returns a list of 256 values, the result of running the values 0 to 255 through a thresholding (or binarization) function, with parameter threshold. This function is defined as:
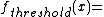
- ::crimp table threshold inside min max
This method returns a list of 256 values, the result of running the values 0 to 255 through a thresholding (or binarization) function, with parameters min and max. This function is defined as:
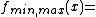
- ::crimp table threshold outside min max
This method returns a list of 256 values, the result of running the values 0 to 255 through a thresholding (or binarization) function, with parameters min and max. This function is defined as:
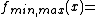
- ::crimp table fgauss discrete sigma ?r?
- ::crimp table fgauss sampled sigma ?r?
This method computes the table for a discrete or sampled gaussian with parameters sigma and kernel radius. If the radius is not specified it defaults to the smallest integer greater than "3*sigma".
- ::crimp transform affine a b c d e f
This method returns the affine transformation specified by the 2x3 matrix
|a b c| |d e f|Note that it is in general easier to use the methods rotate, scale, and translate scale to generate the desired transformation piecemal and then use chain to chain the pieces together.
- ::crimp transform chain transform...
This method computes and returns the projective transformation equivalent to the application of the specified transformations to a 2d point in the given order, i.e with the transformation at the beginning of the argument list applied first, then the one after it, etc.
- ::crimp transform identity
This method returns the projective identity transformation.
- ::crimp transform invert transform
This method computes and returns the inverse of the specified projective transformation.
- ::crimp transform projective a b c d e f g h
This method returns the projective transformation specified by the 3x3 matrix
|a b c| |d e f| |g h 1|Note that for the affine subset of projective transformation it is in general easier to use the methods rotate, scale, and translate scale to generate the desired transformation piecemal and then use chain to chain the pieces together.
And for a true perspective transformation specification through quadrilateral should be simpler as well.
- ::crimp transform quadrilateral src dst
This method returns the projective transformation which maps the quadrilateral src on to the quadrilateral dst.
Each quadrilateral is specified as a list of 4 points, each point a pair of x- and y-coordinates.
The 4 points of each quadrilateral define its corners starting at the top left and going in clock-wise order.
- ::crimp transform reflect line ?a? b
This methods returns the projective transformation which reflects the image about an arbitrary line specified by the two points a and b, each point a pair of x- and y-coordinates.. If point a is not specified it defaults to (0,0), i.e. the coordinate origin.
- ::crimp transform reflect x
This methods returns the projective transformation which reflects the image about the x-axis.
- ::crimp transform reflect y
This methods returns the projective transformation which reflects the image about the y-axis.
- ::crimp transform rotate theta ?center?
This methods returns the projective transformation which rotates the image by the angle theta around the point center. If the latter is not specified {0 0} is assumed. The point, if present, is specified as pair of x- and y-coordinates.
The angle is specified in degrees, with 0 not rotating the image at all. Positive values cause a counterclockwise rotation, negative values a clockwise one.
- ::crimp transform scale sx sy
This methods returns the projective transformation which scales an image by factor sx in width, and sy in height. Values larger than 1 expand the image along the specified dimension, while values less than 1 shrink it. Negative values flip the respective axis.
- ::crimp transform shear sx sy
This methods returns the projective transformation which shears an image by factor sx along the width, and sy along the height.
- ::crimp transform translate dx dy
This methods returns the projective transformation which translates an image by dx pixels along the x-axis, and dx pixels along the y-axis. Values larger than 0 move the image to the right, or down, along the specified dimension, while values less than 0 move it to the left, or up.
Miscellanea
The package contains a number of primitives which are either not really useful to a regular user, or have not gotten a nice interface yet, possibly because it is not clear how that interface should look like.
These primitives are collected here, so that they are not forgotten, i.e. as a reminder to either make them properly available, document as internal/undocumented/etc, or remove them.
- ::crimp::black_white_vertical
Generates a fixed checker board image. The output is 256x256 grey8 image, with 16x16 blocks. Debug use only, so far.
- ::crimp::bilateral_* image sigma-space sigma-range
- ::crimp::joint_bilateral_* image wimage sigma-space sigma-range
Regular and cross bilateral filters. Still looking buggy, possibly bad memory accesses.
- ::crimp::color_combine image vector
This operation combines the channels of the input into a single grey8 value, the result of performing a scalar product of each pixel with the 3x1 vector (float image).
- ::crimp::color_mix image matrix
This operation mixes the color channels of the input, the result of performing a matrix multiplication of each pixel with the 3x3 matrix (float image).
- ::crimp::connected_components image 8connected
- ::crimp::connected_components_* image 8connected bgValue
Computing (labeling) the connected components of the input image, using either 4- or 8-neighbourhood. The primitives accepting a background value use it to distinguish foreground and background and coalesce the latter into a single component, even if its area is disconnected.
The result is always of type grey32, to have enough range for the label counters.
- ::crimp::euclidean_distance_map_float image
- ::crimp::indicator_grey8_float image
These two operations together allow the creation of distance maps from images, i.e. watershed diagrams. Currently only used in a demonstration for this.
- ::crimp::hough_grey8 image emptybucketcolor
Hough transformation of an image. Currently only used in a demonstration so far.
- ::crimp::gaussian_01_float image derivative sigma
- ::crimp::gaussian_10_float image derivative sigma
- ::crimp::gaussian_blur_float image sigma
- ::crimp::gaussian_laplacian_float image sigma
- ::crimp::gaussian_gradient_mag_float image sigma
Fast gaussian filters and derivatives, applied in X and Y directions, i.e. rows and coluimns of the input image. The derivative is either
- 0
Gaussian
- 1
Gradient
- 2
Laplacian
The methods 01 and 10 apply a gaussian or derivative to the image, in X and Y directions, respectively. I.e. they operate on the rows, or columns of the image, respectively.
blur applies a gaussian blur in both directions, i.e.
output = gauss10 (gauss01 (image))laplacian returns an approximation of the scalar second derivative, the laplacian of the image. It is computed by applying a laplacian of a gaussian, for both X and Y directions, and adding the results, i.e.:
laplace20 (gauss01 (image)) + laplace02 (gauss20 (image))gradient_mag returns the magnitude of the image gradient. It is computed by applying a gradient of gaussian to X and Y directions, and computing the length of the resulting 2-vector (euclidean norm), i.e.
hypot (gauss10 (grad10 (image)), gauss10 (grad01 (image)))- ::crimp::map_2*_* image map
Operators applying a piecewise linear map to the input image. The map is stored in a Tcl list containing 2 elements, each a bytearray. The first stores the abscissaes delineating the intervals, the second the ordinates at these interval borders. The format of the binary data depends on the types of input and output values (byte, int, float, ...).
For conversion a pixel value is searched for in the intervals of abscissae. With both the interval and the fraction inside of it known the output is then linearly interpolated from the associated ordinates. The search is a binary one, assuming that the abscissae are sorted from smaller to larger. If the input value is outside of the defined intervals the outputs associated with the min and max abscissae are returned, respectively.
Not exposed yet, unclear how the higher level API should look like.
- ::crimp::map2_* image mapNimage... mapNcontrol...
Primitives applying per-pixel transformations to multi-channel images (HSV, RGB, RGBA). Each channel is transformed with one map image per channel, and one integer index per channel selecting the control channel. Each map is a 256x256 grey8 image indexed by the pixel data of the channel to be mapped in X, and the pixel data of the chosen control channel in Y. This enables effects like hue-dependent changes to saturation or value, value dependent color-shifts, etc.
Not exposed yet, unclear how the higher level API should look like.
- ::crimp::region_sum image radius
Takes a summed area table as input and computes the sums for square windows of the radius around each pixel. Time is constant per pixel, independent of the radius, because of the nature of the input. Only used internally so far.
- ::crimp::exp_float image
- ::crimp::log_float image
- ::crimp::log10_float image
- ::crimp::offset_float image offset
- ::crimp::pow_float_float imageBase imageExponent
- ::crimp::scale_float image factor
- ::crimp::sqrt_float image
Only used internally (or demos), in various calculations like arithmetic mean, standard deviation, etc. Might be useful in general, as unary operator.
- ::crimp::non_max_suppression imageMagnitude imageAngle
- ::crimp::trace_hysteresis image low high
Abandoned, part of an older attempt at canny edge detection.
- ::crimp::window_* image
- ::crimp::window_* image
Window the image by decreasing luma from center to the edges using an inverse square law. Currently only used internally, as part of the translational registration. Might be useful in general.
References
Simon Perreault and Patrick Hebert, "Median Filtering in Constant Time", 2007 http://nomis80.org/ctmf.html
Nobuyuki Otsu, "A threshold selection method from gray-level histograms", 1979 http://en.wikipedia.org/wiki/Otsu%27s_method
Leptonica, "The Tophat and H-dome transforms", http://www.leptonica.com/grayscale-morphology.html#TOPHAT-HDOME
P. Peterlin, "Morphological Operations: An Overview", http://www.inf.u-szeged.hu/ssip/1996/morpho/morphology.html
Adrien Bousseau, "Mathematical Morphology", PDF at http://artis.imag.fr/Members/Adrien.Bousseau/morphology/
Keywords
affine, affine transform, alpha, alpha blending, alpha channel, average, binarization, black tophat, blending, canny, chain transforms, charcoal, clockwise, closing, composite blending, composition, computer vision, const expansion, convolution filter, counter-clockwise, cropping, cut region, cyclic wrap expansion, dilation, document processing, edge shrinking, edge-detection, effect, emboss, erosion, expansion, extend expansion, external gradient, extract rectangle, extract region, fast fourier transform, fft, filter, flip, fourier transform, gamma correction, geometry, gradient, histogram, hypot, identity transforms, image, integral image, internal gradient, inverse fourier transform, inversion, invert transforms, log-compression, log-polar transformation, matrix, max, max-filter, mean, mean filter, median, median-filter, middle, min, min-filter, mirror, mirror expansion, montage, morphology, opening, otsu threshold, perspective, perspective transform, photo, pixel mapping, prewitt, projective, projective transform, quadrilateral, rank-order filter, raw transform, rectangle cut, rectangle extraction, reflect, reflect about aix, reflect about line, reflective transforms, region cut, region of interest, remapping, replicate edge expansion, rescale, resize, roberts, rotate, rotate about a point, rotate transforms, rotation, sabattier effect, scale, scale transforms, scaling, scharr, sharpen, shear, shearing transforms, shrinking, sobel, solarization, sqrt-compression, standard deviation filter, statistics, stddev, summed area table, threshold, thresholding, toggle map, tophat, toroidal wrap expansion, transform, transform affine, transform chaining, transform identity, transform inversion, transform perspective, transform projective, transform reflect, transform rotation, transform scale, transform shear, transform translate, transform, fast fourier, transform, fourier, transform, inverse fourier, transformation, log-polar, translate, translate transforms, translation, variance, vector, vector-field, warp, white tophat, windowing, wrap expansion
Copyright
Copyright © 2011 Andreas Kupries
Copyright © 2011 Documentation, Andreas Kupries